Desviación típica: ¿qué es y para qué sirve?


Escrito y verificado por el psicólogo José Padilla
La estadística sirve para sistematizar, recoger y ordenar los datos de un fenómeno, con la finalidad de deducir las leyes que operan en él y así realizar previsiones, tomar decisiones y sacar conclusiones. Su operativa, y sus estadísticos, como la desviación típica, nos permite transformar números en conclusiones. Con ella, podemos describir las variables de una población o realizar inferencias controlando el nivel de error.
Dentro de la estadística, las medidas de dispersión ―como la desviación típica― sirven, en esencia, para dos propósitos. Constituir una referencia para hablar de la heterogeneidad de una población o muestra y para fijar el nivel de error a la hora de hacer inferencias basándose en un nivel de confianza.
Antes de ver más en profundidad el sentido de la desviación típica, vamos a describir otros estadísticos asociados y que también son muy utilizados en el análisis de datos.
La media y la varianza
Por un lado, la media es una medida de tendencia central que, con complementos, pretende ser una representación de una muestra o población en una variable. Es la suma total de valores en una muestra dividida por el número de valores en su muestra.
Por otro lado, la varianza es una medida de dispersión que representa la oscilación de unos datos en relación con su media. Es decir, brinda una medida para saber cómo de cerca se reparten los datos en torno a su centro. Se calcula como la suma de los residuos —diferencia entre valor y media— al cuadrado, divididos entre el total de observaciones.
Para entenderlo mejor, vamos con un ejemplo. A continuación, ponemos una tabla en la que aparecen los vasos fabricados por Jorge cada uno de los días de la semana.
| Días de la semana | Cantidad de vasos fabricados |
| Lunes | 5 |
| Martes | 4 |
| Miércoles | 7 |
| Jueves | 3 |
| Viernes | 6 |
Para calcular la media sumamos la cantidad de vasos fabricados por día: 5+4+7+3+6= 25
Luego, dividimos el resultado entre el número total de datos: 25/5= 5
El promedio de vasos fabricados por Jorge durante los cinco días es de cinco vasos.
Para hallar la varianza, es necesario calcular los residuos al cuadrado y dividirlos entre el total de observaciones. En palabras más simples, le restamos el promedio (5) a las observaciones, que son la cantidad de vasos fabricados al día (5, 4, 7, 3 y 6), y lo elevamos al cuadrado. Luego, sumamos y dividimos entre el número de observaciones (5):
s²= (5-5) ²+ (4-5) ²+ (7-5) ²+ (3-5) ²+ (6-5) ² / 5= 2
La variación de la cantidad de vasos fabricados de un día a otro, en relación con la media, es de dos. Este dato, dicho así, no sirve para mucho. Sin embargo, podemos comparar la varianza obtenida con la de otras semanas y nos haremos una idea de en qué semanas Jorge ha sido más constante en la producción de vasos.
Qué es la desviación típica
La desviación típica es una medida estadística que nos ofrece información sobre la dispersión de unos datos con respecto a la media. Es el promedio de las desviaciones individuales de cada observación con respecto a la media de una distribución. Esta desviación es siempre mayor o igual a cero. Cuando es baja significa que los datos están cerca del promedio y cuando es alta indica que están más alejados del mismo, es decir, están más dispersos.
Una desviación típica de 0, según el ejemplo que hemos puesto, se produciría si Jorge hubiera producido todos los días de la semana una cantidad de vasos que coincidiera con la media. Este es un caso muy raro, ya que es muy raro que todas las personas de un grupo midan lo mismo, pesen lo mismo o prefieran lo mismo. Es decir, lo que esperamos es variabilidad al analizar los datos de una variable.
¿Cómo se calcula?
Una vez que hemos hallado el valor de la media y la varianza de los datos, podemos calcular la desviación típica, calculándole la raíz cuadrada a esta última. Pongamos esto en práctica hallando la desviación típica de la cantidad de vasos fabricados por Jorge en cinco días:
S= √ (5-5) ²+ (4-5) ²+ (7-5) ²+ (3-5) ²+ (6-5) ² / 5= 1.41
Según este resultado, podemos decir que, en promedio, la cantidad de vasos fabricados por día se desvía de la media (5 vasos) en 1.4142 vasos, es decir, Jorge produce un vaso más o uno menos de la media por día. Esto nos permite afirmar que, por lo general, Jorge se mantiene cerca del promedio de producción de vasos.
Este ejemplo ilustra como, a través de esta medida de dispersión, podemos conocer, en promedio, cómo es una población respecto a una variable (más o menos heterogénea).
Si te das cuenta, en muchas ocasiones, los medios de comunicación solo hablan de medias. Esto provoca que le asignemos un valor a una población en una variable, cuando puede existir una gran heterogeneidad; tanta, que en el fondo, ese valor medio no representa a nadie de la población.
Por ejemplo, podría haberse dado el caso de que Jorge no produjera ningún día cinco vasos. Sin embargo, el titular de la noticia podría ser «Jorge fabrica cinco vasos al día». Paradójico, ¿verdad?
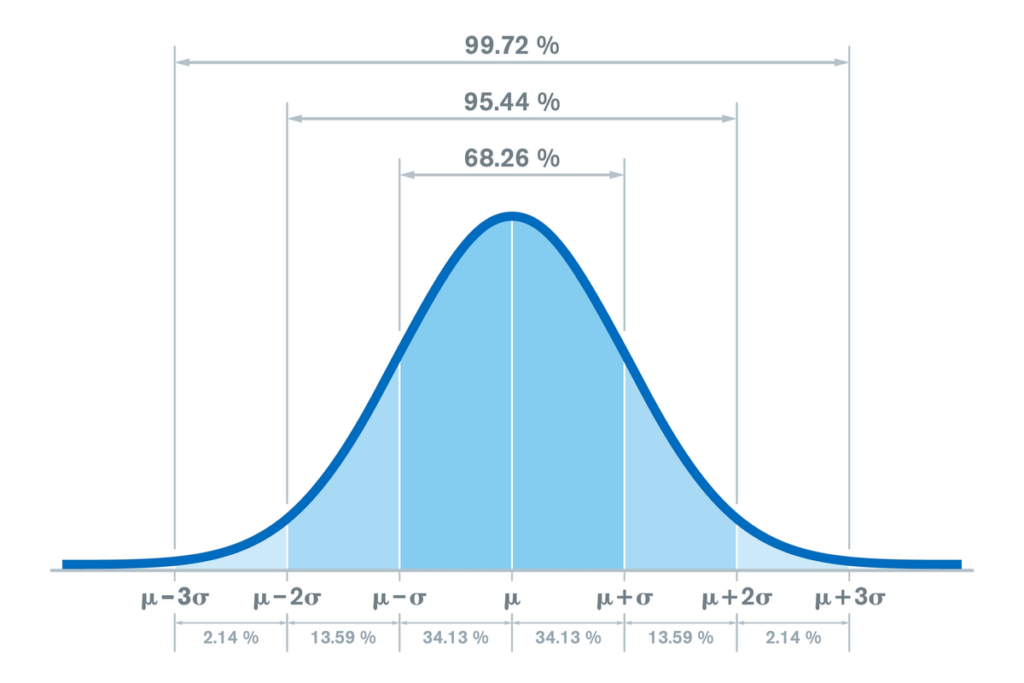
¿Para qué sirve la desviación típica?
Sirve para hacer una estimación sobre cómo de dispersos están los datos con respecto a la media de la variable que se estudia. Nos permiten conocer, en promedio, cómo se concentran las observaciones en torno a la media.
Así, la desviación típica es un índice para usar cuando se pretende describir la variabilidad de una variable continua en una muestra (Abraira, 2002).
Además de servir como referencia para analizar la variabilidad de una población, también sirve para fijar la amplitud del intervalo de confianza al hacer inferencias sobre la media. Cuanto mayor sea la desviación típica, mayor será este intervalo. Esto hace, por ejemplo, que sea más complicado hablar de que existen diferencias significativas entre dos poblaciones.
A nivel psicométrico, se relaciona con la fiabilidad, que en algunos casos puede entenderse como la estabilidad de los resultados obtenidos a lo largo del tiempo en estudios longitudinales. Así, un test sería fiable cuando arroja mediciones muy parecidas para el mismo valor real.
La desviación típica revela la realidad de los datos
La desviación típica nos permite medir la dispersión de los datos con respecto a la media. Asimismo, proporciona información sobre la heterogeneidad de una muestra y es útil para realizar inferencias.
Al calcularla, obtenemos una medida de cuánto se dispersan las observaciones de la media, lo que nos ayuda a entender las fluctuaciones de la variable estudiada. La desviación típica es esencial para evitar conclusiones equivocadas basadas solo en el promedio y nos brinda una perspectiva más completa de los datos.
La estadística sirve para sistematizar, recoger y ordenar los datos de un fenómeno, con la finalidad de deducir las leyes que operan en él y así realizar previsiones, tomar decisiones y sacar conclusiones. Su operativa, y sus estadísticos, como la desviación típica, nos permite transformar números en conclusiones. Con ella, podemos describir las variables de una población o realizar inferencias controlando el nivel de error.
Dentro de la estadística, las medidas de dispersión ―como la desviación típica― sirven, en esencia, para dos propósitos. Constituir una referencia para hablar de la heterogeneidad de una población o muestra y para fijar el nivel de error a la hora de hacer inferencias basándose en un nivel de confianza.
Antes de ver más en profundidad el sentido de la desviación típica, vamos a describir otros estadísticos asociados y que también son muy utilizados en el análisis de datos.
La media y la varianza
Por un lado, la media es una medida de tendencia central que, con complementos, pretende ser una representación de una muestra o población en una variable. Es la suma total de valores en una muestra dividida por el número de valores en su muestra.
Por otro lado, la varianza es una medida de dispersión que representa la oscilación de unos datos en relación con su media. Es decir, brinda una medida para saber cómo de cerca se reparten los datos en torno a su centro. Se calcula como la suma de los residuos —diferencia entre valor y media— al cuadrado, divididos entre el total de observaciones.
Para entenderlo mejor, vamos con un ejemplo. A continuación, ponemos una tabla en la que aparecen los vasos fabricados por Jorge cada uno de los días de la semana.
| Días de la semana | Cantidad de vasos fabricados |
| Lunes | 5 |
| Martes | 4 |
| Miércoles | 7 |
| Jueves | 3 |
| Viernes | 6 |
Para calcular la media sumamos la cantidad de vasos fabricados por día: 5+4+7+3+6= 25
Luego, dividimos el resultado entre el número total de datos: 25/5= 5
El promedio de vasos fabricados por Jorge durante los cinco días es de cinco vasos.
Para hallar la varianza, es necesario calcular los residuos al cuadrado y dividirlos entre el total de observaciones. En palabras más simples, le restamos el promedio (5) a las observaciones, que son la cantidad de vasos fabricados al día (5, 4, 7, 3 y 6), y lo elevamos al cuadrado. Luego, sumamos y dividimos entre el número de observaciones (5):
s²= (5-5) ²+ (4-5) ²+ (7-5) ²+ (3-5) ²+ (6-5) ² / 5= 2
La variación de la cantidad de vasos fabricados de un día a otro, en relación con la media, es de dos. Este dato, dicho así, no sirve para mucho. Sin embargo, podemos comparar la varianza obtenida con la de otras semanas y nos haremos una idea de en qué semanas Jorge ha sido más constante en la producción de vasos.
Qué es la desviación típica
La desviación típica es una medida estadística que nos ofrece información sobre la dispersión de unos datos con respecto a la media. Es el promedio de las desviaciones individuales de cada observación con respecto a la media de una distribución. Esta desviación es siempre mayor o igual a cero. Cuando es baja significa que los datos están cerca del promedio y cuando es alta indica que están más alejados del mismo, es decir, están más dispersos.
Una desviación típica de 0, según el ejemplo que hemos puesto, se produciría si Jorge hubiera producido todos los días de la semana una cantidad de vasos que coincidiera con la media. Este es un caso muy raro, ya que es muy raro que todas las personas de un grupo midan lo mismo, pesen lo mismo o prefieran lo mismo. Es decir, lo que esperamos es variabilidad al analizar los datos de una variable.
¿Cómo se calcula?
Una vez que hemos hallado el valor de la media y la varianza de los datos, podemos calcular la desviación típica, calculándole la raíz cuadrada a esta última. Pongamos esto en práctica hallando la desviación típica de la cantidad de vasos fabricados por Jorge en cinco días:
S= √ (5-5) ²+ (4-5) ²+ (7-5) ²+ (3-5) ²+ (6-5) ² / 5= 1.41
Según este resultado, podemos decir que, en promedio, la cantidad de vasos fabricados por día se desvía de la media (5 vasos) en 1.4142 vasos, es decir, Jorge produce un vaso más o uno menos de la media por día. Esto nos permite afirmar que, por lo general, Jorge se mantiene cerca del promedio de producción de vasos.
Este ejemplo ilustra como, a través de esta medida de dispersión, podemos conocer, en promedio, cómo es una población respecto a una variable (más o menos heterogénea).
Si te das cuenta, en muchas ocasiones, los medios de comunicación solo hablan de medias. Esto provoca que le asignemos un valor a una población en una variable, cuando puede existir una gran heterogeneidad; tanta, que en el fondo, ese valor medio no representa a nadie de la población.
Por ejemplo, podría haberse dado el caso de que Jorge no produjera ningún día cinco vasos. Sin embargo, el titular de la noticia podría ser «Jorge fabrica cinco vasos al día». Paradójico, ¿verdad?

¿Para qué sirve la desviación típica?
Sirve para hacer una estimación sobre cómo de dispersos están los datos con respecto a la media de la variable que se estudia. Nos permiten conocer, en promedio, cómo se concentran las observaciones en torno a la media.
Así, la desviación típica es un índice para usar cuando se pretende describir la variabilidad de una variable continua en una muestra (Abraira, 2002).
Además de servir como referencia para analizar la variabilidad de una población, también sirve para fijar la amplitud del intervalo de confianza al hacer inferencias sobre la media. Cuanto mayor sea la desviación típica, mayor será este intervalo. Esto hace, por ejemplo, que sea más complicado hablar de que existen diferencias significativas entre dos poblaciones.
A nivel psicométrico, se relaciona con la fiabilidad, que en algunos casos puede entenderse como la estabilidad de los resultados obtenidos a lo largo del tiempo en estudios longitudinales. Así, un test sería fiable cuando arroja mediciones muy parecidas para el mismo valor real.
La desviación típica revela la realidad de los datos
La desviación típica nos permite medir la dispersión de los datos con respecto a la media. Asimismo, proporciona información sobre la heterogeneidad de una muestra y es útil para realizar inferencias.
Al calcularla, obtenemos una medida de cuánto se dispersan las observaciones de la media, lo que nos ayuda a entender las fluctuaciones de la variable estudiada. La desviación típica es esencial para evitar conclusiones equivocadas basadas solo en el promedio y nos brinda una perspectiva más completa de los datos.
Todas las fuentes citadas fueron revisadas a profundidad por nuestro equipo, para asegurar su calidad, confiabilidad, vigencia y validez. La bibliografía de este artículo fue considerada confiable y de precisión académica o científica.
- Abraira, V. (2002). Desviación estándar y error estándar. SEMERGEN-Medicina de Familia, 28(11), 621-623. https://www.elsevier.es/es-revista-medicina-familia-semergen-40-articulo-desviacion-estandar-error-estandar-S1138359302741385
- Hurley, M., & Tenny, S. (2022). Mean. StatPearls. Consultado el 28 de julio de 2023. https://www.ncbi.nlm.nih.gov/books/NBK546702/ https://www.ncbi.nlm.nih.gov/books/NBK546702/
- National Library of Medicine. (s.f.). Standard Deviation. Consultado el 28 de julio de 2023. https://www.nlm.nih.gov/nichsr/stats_tutorial/section2/mod8_sd.html#:~:text=A%20standard%20deviation%20(or%20%CF%83,data%20are%20more%20spread%20out.
- López, J.F. (02 de octubre, 2017). Desviación estándar o típica. Economipedia. Consultado el 13 de octubre de 2021. https://economipedia.com/definiciones/desviacion-tipica.html
- Salazar, C. y Del Castillo, S. (2017). Fundamentos básicos de estadística. Sin editorial.
- The BMJ. (s.f.). Mean and standard deviation. Consultado el 13 de octubre de 2021. https://www.bmj.com/about-bmj/resources-readers/publications/statistics-square-one/2-mean-and-standard-deviation
- Wadhwa, R. R., & Azzam, D. (2019). Variance. StatPearls. Consultado el 28 de julio de 2023. https://www.ncbi.nlm.nih.gov/books/NBK551689/#:~:text=Although%20the%20arithmetic%20mean%20of,spread%20around%20its%20center.%5B2
Este texto se ofrece únicamente con propósitos informativos y no reemplaza la consulta con un profesional. Ante dudas, consulta a tu especialista.







