¿Qué harías tú en el dilema del prisionero?


Revisado y aprobado por el psicólogo Sergio De Dios González
El dilema del prisionero es un problema fundamental de la teoría de juegos. Muestra que las personas pueden elegir no cooperar, aunque esa decisión vaya en contra de sus intereses. Con este juego, se analizan las decisiones que toman dos presos encarcelados por un delito menor, cuando se les ofrece la posibilidad de delatar a su compañero a la policía.
Si un preso colabora con la policía, este obtendrá beneficios penitenciarios. Estos beneficios serán mayores o menores dependiendo de la decisión que el otro preso tome. En este juego se presupone que cada prisionero está encarcelado por separado. De esta forma que no pueden comunicarse entre ellos, ni saber la decisión del otro.
Por consiguiente, los presos no pueden pactar sus decisiones ni saber que es lo que el otro preso va a hacer. Así, acertar con la decisión que tomará el otro prisionero va a ser fundamental a la hora de anticipar las consecuencias de la propia decisión.
“¿Puede extrañar que la prisión se asemeje a las fábricas, a las escuelas, a los cuarteles, a los hospitales, todos los cuales se asemejan a las prisiones?”
-Michel Foucault-
Posibles decisiones ante el dilema del prisionero
Las posibilidades que ambos presos tienen son dos: delatar a su compañero o no delatarlo. Es la base y el punto de inicio del juego. Por tanto, teniendo en cuenta las dos decisiones que cada uno de los presos puede tomar, se definen un total de cuatro posibilidades que pueden darse dependiendo de las decisiones de ambos presos.
- Ninguno de los dos presos delata a su compañero. En este caso, cada preso recibiría solo dos años de cárcel (-2, -2).
- Solo uno de los presos delata a su compañero. En este caso, el prisionero que delata a su compañero sería condenado a solo un año de cárcel, mientras que el prisionero que no delata a su compañero sería condenado a diez (-10, -1 o -1, -10).
- Los dos presos delatan a su compañero. En este caso, la condena de cárcel para cada uno de ellos sería de seis años (-6, -6).
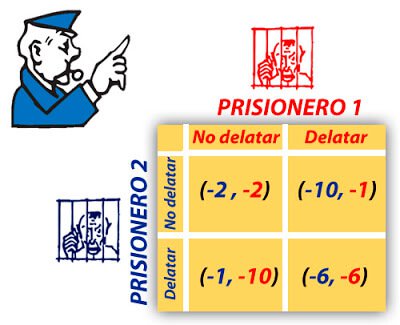
Repercusión de las decisiones en el dilema del prisionero
Hay una condición que tenemos que tener en cuenta si jugamos a este juego, y es que cada prisionero va a querer lo mejor para él, sin importarle qué le suceda a su compañero. A primera vista, si nos introducimos en la piel de uno de los dos prisioneros. Por lo tanto, la mejor decisión sería delatar al otro prisionero, pues en todos los casos las condenas serían más bajas.
Siguiendo este tipo de lógica, es de suponer que el otro prisionero piense lo mismo y acabe por delatarnos. En este caso, como los dos nos hemos delatado mutuamente, la condena de cárcel sería de seis años para cada uno. Si, por el contrario, los dos hubiéramos decidido cooperar y no delatarnos, las condenas habrían sido menores, solo de dos años.
El equilibrio de Nash
La situación que se plantea con este juego se denomina un “equilibrio de Nash”. El nombre viene dado por el matemático Jonh Forbes Nash, conocido entre el público general por la película que da nombre a este blog, “Una mente maravillosa”.
En esta situación de “equilibrio de Nash”, cada jugador individual no gana nada si modifica su estrategia mientras que los otros jugadores no cambian las suyas. Por ello, cambiar la decisión individual implica empeorar las condiciones. Así, cada jugador ejecuta el mejor movimiento que pueda dados los movimientos de los demás jugadores.
Al no poder coordinar las decisiones con los demás jugadores, la mejor decisión que se puede tomar va a ser la que permita más beneficios individualmente. No obstante, esta decisión no será la mejor para el conjunto de jugadores.
Variantes del juego del dilema del prisionero
El dilema del prisionero también presenta distintas variantes en las que pueden participar más jugadores. Algunas de estas son las siguientes:
1. Piedra, papel o tijera
Este juego quizás sea el más conocido por su uso popular a la hora de tomar decisiones sobre preferencias. Aunque este juego no es una variante del dilema del prisionero, sí que presenta un “equilibrio de Nash” ya que cada opción elegida tiene un tercio de posibilidades y que sea ganadora o perdedora va a depender de lo que haga el otro.
2. Juego de confianza
Es un juego secuencial en que un jugador decide primero su nivel de confianza en el segundo jugador. A mayor confianza mayor es el pago que se genera para el segundo jugador. Seguidamente, debe decidir si corresponde la confianza con una decisión que es mutuamente beneficiosa para los dos.
3. Amigo o enemigo
En este juego compiten tres pares de personas. Cuando cada pareja es eliminada, juegan a un juego del dilema del prisionero para determinar cómo se reparten sus ganancias. Si ambos cooperan (“amigo”), comparten sus beneficios al 50%. Cuando uno coopera y el otro deserta (“enemigo”), el desertor se lleva todas las ganancias y el cooperador ninguna. Y si ambos desertan, ninguno se lleva nada.
La aplicación del dilema del prisionero
El dilema del prisionero es un juego simple que ha permitido a los investigadores conocer mejor cómo tomamos decisiones. Aunque pensamos que las decisiones lógicas, como en este caso delatar al otro preso, que nos van a aportar más beneficios son las correctas y por las que la gente suele optar, otras decisiones no tan lógicas, como no delatarlo, nos pueden dar más beneficios, teniendo en cuenta que las demás personas tampoco opten por decisiones lógicas.
En conclusión, las decisiones que tomamos no son tan simples y dependen de muchos factores. Así, las decisiones que tomamos habitualmente no suelen parecer lógicas a primera vista. Para encontrar su lógica hay que profundizar más en esa serie de factores y cogniciones que nos llevan a optar por esas decisiones en detrimento de otras más lógicas.
Finalmente, les dejamos con una frase de John Forbes Nash:
“Siempre he creído en los números. En las ecuaciones y la lógica que llevan a la razón. Pero, después de una vida de búsqueda me digo, ¿Qué es la lógica? ¿Quién decide la razón?”
El dilema del prisionero es un problema fundamental de la teoría de juegos. Muestra que las personas pueden elegir no cooperar, aunque esa decisión vaya en contra de sus intereses. Con este juego, se analizan las decisiones que toman dos presos encarcelados por un delito menor, cuando se les ofrece la posibilidad de delatar a su compañero a la policía.
Si un preso colabora con la policía, este obtendrá beneficios penitenciarios. Estos beneficios serán mayores o menores dependiendo de la decisión que el otro preso tome. En este juego se presupone que cada prisionero está encarcelado por separado. De esta forma que no pueden comunicarse entre ellos, ni saber la decisión del otro.
Por consiguiente, los presos no pueden pactar sus decisiones ni saber que es lo que el otro preso va a hacer. Así, acertar con la decisión que tomará el otro prisionero va a ser fundamental a la hora de anticipar las consecuencias de la propia decisión.
“¿Puede extrañar que la prisión se asemeje a las fábricas, a las escuelas, a los cuarteles, a los hospitales, todos los cuales se asemejan a las prisiones?”
-Michel Foucault-
Posibles decisiones ante el dilema del prisionero
Las posibilidades que ambos presos tienen son dos: delatar a su compañero o no delatarlo. Es la base y el punto de inicio del juego. Por tanto, teniendo en cuenta las dos decisiones que cada uno de los presos puede tomar, se definen un total de cuatro posibilidades que pueden darse dependiendo de las decisiones de ambos presos.
- Ninguno de los dos presos delata a su compañero. En este caso, cada preso recibiría solo dos años de cárcel (-2, -2).
- Solo uno de los presos delata a su compañero. En este caso, el prisionero que delata a su compañero sería condenado a solo un año de cárcel, mientras que el prisionero que no delata a su compañero sería condenado a diez (-10, -1 o -1, -10).
- Los dos presos delatan a su compañero. En este caso, la condena de cárcel para cada uno de ellos sería de seis años (-6, -6).

Repercusión de las decisiones en el dilema del prisionero
Hay una condición que tenemos que tener en cuenta si jugamos a este juego, y es que cada prisionero va a querer lo mejor para él, sin importarle qué le suceda a su compañero. A primera vista, si nos introducimos en la piel de uno de los dos prisioneros. Por lo tanto, la mejor decisión sería delatar al otro prisionero, pues en todos los casos las condenas serían más bajas.
Siguiendo este tipo de lógica, es de suponer que el otro prisionero piense lo mismo y acabe por delatarnos. En este caso, como los dos nos hemos delatado mutuamente, la condena de cárcel sería de seis años para cada uno. Si, por el contrario, los dos hubiéramos decidido cooperar y no delatarnos, las condenas habrían sido menores, solo de dos años.
El equilibrio de Nash
La situación que se plantea con este juego se denomina un “equilibrio de Nash”. El nombre viene dado por el matemático Jonh Forbes Nash, conocido entre el público general por la película que da nombre a este blog, “Una mente maravillosa”.
En esta situación de “equilibrio de Nash”, cada jugador individual no gana nada si modifica su estrategia mientras que los otros jugadores no cambian las suyas. Por ello, cambiar la decisión individual implica empeorar las condiciones. Así, cada jugador ejecuta el mejor movimiento que pueda dados los movimientos de los demás jugadores.
Al no poder coordinar las decisiones con los demás jugadores, la mejor decisión que se puede tomar va a ser la que permita más beneficios individualmente. No obstante, esta decisión no será la mejor para el conjunto de jugadores.
Variantes del juego del dilema del prisionero
El dilema del prisionero también presenta distintas variantes en las que pueden participar más jugadores. Algunas de estas son las siguientes:
1. Piedra, papel o tijera
Este juego quizás sea el más conocido por su uso popular a la hora de tomar decisiones sobre preferencias. Aunque este juego no es una variante del dilema del prisionero, sí que presenta un “equilibrio de Nash” ya que cada opción elegida tiene un tercio de posibilidades y que sea ganadora o perdedora va a depender de lo que haga el otro.
2. Juego de confianza
Es un juego secuencial en que un jugador decide primero su nivel de confianza en el segundo jugador. A mayor confianza mayor es el pago que se genera para el segundo jugador. Seguidamente, debe decidir si corresponde la confianza con una decisión que es mutuamente beneficiosa para los dos.
3. Amigo o enemigo
En este juego compiten tres pares de personas. Cuando cada pareja es eliminada, juegan a un juego del dilema del prisionero para determinar cómo se reparten sus ganancias. Si ambos cooperan (“amigo”), comparten sus beneficios al 50%. Cuando uno coopera y el otro deserta (“enemigo”), el desertor se lleva todas las ganancias y el cooperador ninguna. Y si ambos desertan, ninguno se lleva nada.
La aplicación del dilema del prisionero
El dilema del prisionero es un juego simple que ha permitido a los investigadores conocer mejor cómo tomamos decisiones. Aunque pensamos que las decisiones lógicas, como en este caso delatar al otro preso, que nos van a aportar más beneficios son las correctas y por las que la gente suele optar, otras decisiones no tan lógicas, como no delatarlo, nos pueden dar más beneficios, teniendo en cuenta que las demás personas tampoco opten por decisiones lógicas.
En conclusión, las decisiones que tomamos no son tan simples y dependen de muchos factores. Así, las decisiones que tomamos habitualmente no suelen parecer lógicas a primera vista. Para encontrar su lógica hay que profundizar más en esa serie de factores y cogniciones que nos llevan a optar por esas decisiones en detrimento de otras más lógicas.
Finalmente, les dejamos con una frase de John Forbes Nash:
“Siempre he creído en los números. En las ecuaciones y la lógica que llevan a la razón. Pero, después de una vida de búsqueda me digo, ¿Qué es la lógica? ¿Quién decide la razón?”
Todas las fuentes citadas fueron revisadas a profundidad por nuestro equipo, para asegurar su calidad, confiabilidad, vigencia y validez. La bibliografía de este artículo fue considerada confiable y de precisión académica o científica.
- Axelrod, R. (1986). La evolución de la cooperación: el Dilema del Prisionero y la teoría de los juegos (No. 334/A96eE).
- Contreras, J. M., Batanero, C., Arteaga, P., & Cañadas, G. (2011). El dilema de los prisioneros: valor de las paradojas en la clase de matemáticas. Gamma: revista galega de educación matemática, 12, 31-37.
- Gómez, I., González, J. M., & Cardona, T. (1976). Relación entre la cooperación en el dilema del prisionero y las escalas E (intro-extraversión), N (neuroticismo) y P (psicoticismo). Revista Latinoamericana de Psicología, 8(1), 25-29.
- Poundstone, W. (1995). El dilema del prisionero: John von Neumann, la teoría de juegos y la bomba. Alianza.
Este texto se ofrece únicamente con propósitos informativos y no reemplaza la consulta con un profesional. Ante dudas, consulta a tu especialista.







