El teorema de Bayes


Escrito y verificado por el psicólogo Sergio De Dios González
El teorema de Bayes constituye uno de los pilares de la probabilidad. Se trata de una teoría planteada por Thomas Bayes (1702-1761) en el siglo XVIII. Pero, ¿Qué trata de explicar el científico exactamente? Según la Real Academia Española, la probabilidad expresa, en un proceso aleatorio, la razón entre el número de casos favorables y el número de casos posibles.
Así, alrededor de la probabilidad se han desarrollado muchas teorías que hoy nos gobiernan. Cuando vamos al médico nos receta aquello que es más probable que nos venga bien, los publicistas dedican sus campañas a las personas que es más probable que adquieran el producto que quieran promocionar, nosotros elegimos el recorrido por el que es más probable que tardemos menos
Una de las leyes más famosas de probabilidad es la ley de la probabilidad total. Para comenzar, hemos de tener en cuenta de qué trata la ley de la probabilidad total. Para comprenderla, pongamos un ejemplo.
Pongamos que, en un país aleatorio, el 39% de la población son mujeres. Sabemos también que un 22 % de las mujeres y un 14% de los hombres están en paro. Entonces, ¿cuál es la probabilidad (P) de que una persona elegida al azar de la población activa en este país se encuentre en paro?

Según la teoría de la probabilidad, los datos se expresarían de la siguiente manera:
- La probabilidad de que la persona fuese mujer: P(M)
- La probabilidad de que la persona fuese hombre: P(H)
Sabiendo que el 39% de la población son mujeres, entonces deducimos que: P(M) = 0.39.
Luego, entendemos que: P(H) = 1 – 0.39 = 0.61. También el problema plateado nos da las probabilidades condicionales:
- Probabilidad de que una persona este en paro, sabiendo que es mujer —> P (P|M) = 0.22
- Probabilidad de que una persona este en paro, sabiendo que es hombre —- P (P|H) = 0.14
De esta manera, utilizando la ley de la probabilidad total tendremos:
P (P) = P(M)P(P|M) + P(H)P(P|H)
P (P) = 0.22 × 0.39 + 0.14 × 0.61
P (P) = 0.17
Así, la probabilidad de que una persona elegida al azar se encuentre en paro será de 0.17. Observamos que el resultado se encuentra entre las dos probabilidades condicionales (0.22<0.17<0.14). Además, está más cerca de los hombres porque en la población de este país inventado son mayoría.
El teorema de Bayes
Bien, ahora supongamos que se elige una persona adulta aleatoriamente para rellenar un formulario y se observa que no tiene trabajo. En este caso, y teniendo en cuenta el ejemplo anterior, ¿Cuál es la probabilidad de que esta persona elegida aleatoriamente sea una mujer -P (M|P)-?
Para resolver este problema aplicaremos el teorema de Bayes. Así, este teorema es utilizado para calcular la probabilidad de un suceso teniendo información de antemano sobre ese suceso. Podemos calcular la probabilidad de un suceso A, sabiendo además que ese suceso A cumple con cierta característica (B) que condiciona su probabilidad.
En este caso, hablamos de la probabilidad de que la persona elegida aleatoriamente para rellenar un formulario sea mujer. Pero además, esta probabilidad no será independiente de que la persona seleccionada esté en paro o no.
La fórmula del teorema de Bayes
Como cualquier otro teorema, para calcular la probabilidad necesitamos una fórmula. En este tipo de sucesos, la fórmula se define así:
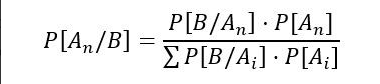
Parece complicado pero todo tiene una explicación. Vayamos por partes. ¿Qué significa cada letra?
- Para comenzar, B es el suceso sobre el que tenemos información previa.
- Por su parte, la letra A(n) hace referencia a los distintos sucesos condicionados.
- En la parte del numerador tenemos la probabilidad condicionada. Esta hace referencia a la probabilidad de que algo (un evento A) ocurra, sabiendo que también ocurre otro evento (B). Se define como P(A|B) y se expresa como: La probabilidad de A dado B.
- En el denominador, tenemos el equivalente a P(B). Ver el apartado anterior.

Un ejemplo:
Así pues, volviendo al ejemplo anterior, supongamos que se elige un adulto al azar para rellenar un cuestionario y se observa que no tiene trabajo (Está en paro). ¿Cuál será la probabilidad de que esta persona elegida sea mujer?
Pues bien, teniendo en cuenta el ejemplo anterior, sabemos que el 39 % de la población activa son mujeres. Sabemos, entonces, que el resto son hombres. Además, sabemos que el porcentaje de mujeres paradas es del 22% y de hombres es del 14%.
Por último, también sabemos que la probabilidad de que una persona elegida al azar esté en paro es de 0.17. Entonces, si aplicamos la fórmula del teorema de Bayes, el resultado que obtendremos es que hay un 0.5 de probabilidad de que una persona elegida al azar, de entre todos los que está en paro, sea mujer.
P(M|P) = (P(M) * P (P|M)/P(P)) = (0,22 * 0,39)/0,17 = 0,5
Despidamos este artículo probabilidad aludiendo a una de las confusiones más frecuentes respecto a la probabilidad. Esta oscila entre 1 y 0, no saliéndose nunca de estos márgenes; siendo 1 la probabilidad de un suceso seguro y 0 la probabilidad de un suceso imposible.
El teorema de Bayes constituye uno de los pilares de la probabilidad. Se trata de una teoría planteada por Thomas Bayes (1702-1761) en el siglo XVIII. Pero, ¿Qué trata de explicar el científico exactamente? Según la Real Academia Española, la probabilidad expresa, en un proceso aleatorio, la razón entre el número de casos favorables y el número de casos posibles.
Así, alrededor de la probabilidad se han desarrollado muchas teorías que hoy nos gobiernan. Cuando vamos al médico nos receta aquello que es más probable que nos venga bien, los publicistas dedican sus campañas a las personas que es más probable que adquieran el producto que quieran promocionar, nosotros elegimos el recorrido por el que es más probable que tardemos menos
Una de las leyes más famosas de probabilidad es la ley de la probabilidad total. Para comenzar, hemos de tener en cuenta de qué trata la ley de la probabilidad total. Para comprenderla, pongamos un ejemplo.
Pongamos que, en un país aleatorio, el 39% de la población son mujeres. Sabemos también que un 22 % de las mujeres y un 14% de los hombres están en paro. Entonces, ¿cuál es la probabilidad (P) de que una persona elegida al azar de la población activa en este país se encuentre en paro?

Según la teoría de la probabilidad, los datos se expresarían de la siguiente manera:
- La probabilidad de que la persona fuese mujer: P(M)
- La probabilidad de que la persona fuese hombre: P(H)
Sabiendo que el 39% de la población son mujeres, entonces deducimos que: P(M) = 0.39.
Luego, entendemos que: P(H) = 1 – 0.39 = 0.61. También el problema plateado nos da las probabilidades condicionales:
- Probabilidad de que una persona este en paro, sabiendo que es mujer —> P (P|M) = 0.22
- Probabilidad de que una persona este en paro, sabiendo que es hombre —- P (P|H) = 0.14
De esta manera, utilizando la ley de la probabilidad total tendremos:
P (P) = P(M)P(P|M) + P(H)P(P|H)
P (P) = 0.22 × 0.39 + 0.14 × 0.61
P (P) = 0.17
Así, la probabilidad de que una persona elegida al azar se encuentre en paro será de 0.17. Observamos que el resultado se encuentra entre las dos probabilidades condicionales (0.22<0.17<0.14). Además, está más cerca de los hombres porque en la población de este país inventado son mayoría.
El teorema de Bayes
Bien, ahora supongamos que se elige una persona adulta aleatoriamente para rellenar un formulario y se observa que no tiene trabajo. En este caso, y teniendo en cuenta el ejemplo anterior, ¿Cuál es la probabilidad de que esta persona elegida aleatoriamente sea una mujer -P (M|P)-?
Para resolver este problema aplicaremos el teorema de Bayes. Así, este teorema es utilizado para calcular la probabilidad de un suceso teniendo información de antemano sobre ese suceso. Podemos calcular la probabilidad de un suceso A, sabiendo además que ese suceso A cumple con cierta característica (B) que condiciona su probabilidad.
En este caso, hablamos de la probabilidad de que la persona elegida aleatoriamente para rellenar un formulario sea mujer. Pero además, esta probabilidad no será independiente de que la persona seleccionada esté en paro o no.
La fórmula del teorema de Bayes
Como cualquier otro teorema, para calcular la probabilidad necesitamos una fórmula. En este tipo de sucesos, la fórmula se define así:
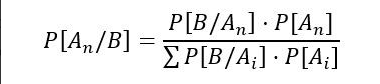
Parece complicado pero todo tiene una explicación. Vayamos por partes. ¿Qué significa cada letra?
- Para comenzar, B es el suceso sobre el que tenemos información previa.
- Por su parte, la letra A(n) hace referencia a los distintos sucesos condicionados.
- En la parte del numerador tenemos la probabilidad condicionada. Esta hace referencia a la probabilidad de que algo (un evento A) ocurra, sabiendo que también ocurre otro evento (B). Se define como P(A|B) y se expresa como: La probabilidad de A dado B.
- En el denominador, tenemos el equivalente a P(B). Ver el apartado anterior.

Un ejemplo:
Así pues, volviendo al ejemplo anterior, supongamos que se elige un adulto al azar para rellenar un cuestionario y se observa que no tiene trabajo (Está en paro). ¿Cuál será la probabilidad de que esta persona elegida sea mujer?
Pues bien, teniendo en cuenta el ejemplo anterior, sabemos que el 39 % de la población activa son mujeres. Sabemos, entonces, que el resto son hombres. Además, sabemos que el porcentaje de mujeres paradas es del 22% y de hombres es del 14%.
Por último, también sabemos que la probabilidad de que una persona elegida al azar esté en paro es de 0.17. Entonces, si aplicamos la fórmula del teorema de Bayes, el resultado que obtendremos es que hay un 0.5 de probabilidad de que una persona elegida al azar, de entre todos los que está en paro, sea mujer.
P(M|P) = (P(M) * P (P|M)/P(P)) = (0,22 * 0,39)/0,17 = 0,5
Despidamos este artículo probabilidad aludiendo a una de las confusiones más frecuentes respecto a la probabilidad. Esta oscila entre 1 y 0, no saliéndose nunca de estos márgenes; siendo 1 la probabilidad de un suceso seguro y 0 la probabilidad de un suceso imposible.
Todas las fuentes citadas fueron revisadas a profundidad por nuestro equipo, para asegurar su calidad, confiabilidad, vigencia y validez. La bibliografía de este artículo fue considerada confiable y de precisión académica o científica.
- 4. PROBABILIDAD CONDICIONADA Y EL TEOREMA DE BAYES. Retrieved from http://webcache.googleusercontent.com/search?q=cache:0EF2amyeIKMJ:halweb.uc3m.es/esp/Personal/personas/mwiper/docencia/Spanish/Teoria_Est_El/tema4_orig.pdf+&cd=13&hl=es&ct=clnk&gl=es&client=firefox-b-ab
-
Díaz, C., & de la Fuente, I. (2006). Enseñanza del teorema de Bayes con apoyo tecnológico. Investigación en el aula de matemáticas. Estadística y Azar.
- Teorema de Bayes – Definición, qué es y concepto | Economipedia. Retrieved from https://economipedia.com/definiciones/teorema-de-bayes.html
Este texto se ofrece únicamente con propósitos informativos y no reemplaza la consulta con un profesional. Ante dudas, consulta a tu especialista.







